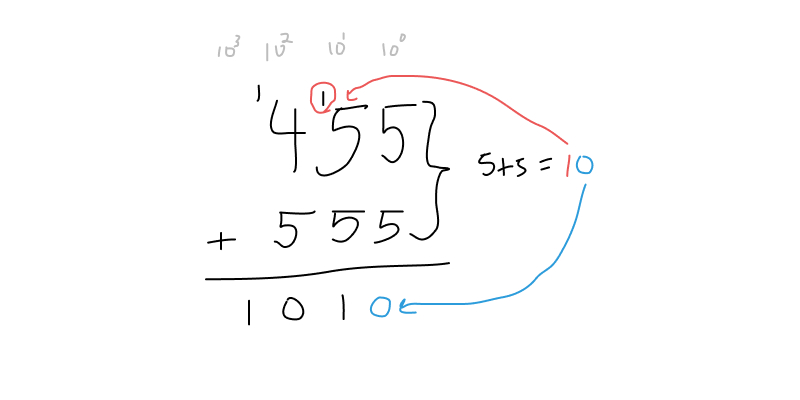Supporting Arbitrary-Precision Integers in JavaScript
The Google Chrome team recently announced that they’re adding support for arbitrary precision integers. This opens up JavaScript to natively support some use cases that previously relied on user libraries. Some of these use cases include:
- handling IDs that are larger than the maximum precise integer by JavaScript’s
Number(253) - handling timestamps with higher precision
- using JavaScript for cryptographic algorithms that rely on extremely large prime numbers
Before their announcement, I was working on implementing a message encryption/decryption module using the RSA algorithm written in Node.js to learn more about cryptography, and started going down a rabbit-hole on how to handle large integers in JavaScript without native support. In my exploration, I looked at a lot of user libraries that handle big integers (mostly Peter Olsen’s BigInteger.js), but also decided to work on my own partial implementation of these libraries to better understand how to work with large integers in any language that doesn’t support them natively. This post is an attempt to consolidate what I learned.
Note: I’m trying to make this resource as understandable as possible to people who are just learning to program in JavaScript, so if you have questions or want something clarified, tweet me, and I may update the post to reflect your feedback.
Before I get into the data structures and algorithms for handling large integers, let’s take a very high-level look at how JavaScript currently handles numbers under the hood.
A Quick Jump into Floating Point Numbers
Note: for simplicity’s sake and for the understanding of people who are less familiar with binary, I will be referring to most numbers in this post using powers of ten/the decimal system instead of powers of two.
Under the hood, all JavaScript integers are a type of data representation called a 64-bit floating point numbers. If that’s unfamiliar terminology, here’s what this means:
- 64-bit refers to the total size that is allowed for representing numbers. As we’ll see in a minute, this includes the significant figures of the number, but in the case of the floating point data type, it also includes information about where we put the decimal point and whether the number is positive or negative.
- floating point is a term that is used for numbers that include integers, but also numbers with a fractional value (e.g. numbers with a decimal point that have nonzero values after it). The floating part refers to the fact that the decimal point is not fixed as it is with integers.

Floating point numbers are kind of a pain to fully grasp, so I don’t want to get too deep into the details of how they work, and how they’re represented in hardware (if you’re interested in learning more, I recommend starting with this Computerphile video on the subject, and there are also much denser resources on the subject if that’s your kinda thing). But it’s important to at least understand the limitations that a 64-bit floating point value has for representing integers in JavaScript.
Limitations of Floating Point Numbers
As we mentioned earlier, the 64-bit part of JavaScript’s internal representation of numbers means that we only have that much space to represent all information about our number, including where the decimal goes and whether the number is negative or positive. In JavaScript, this is how those bits are used:
- 1 bit is used as the sign bit or the bit that tells us whether the number is positive or negative
- 11 bits are used to represent the exponent, which can be either positive and negative, allowing for fractions (e.g., 10-1 is
0.1) - 52 bits are used for the mantissa, which is a mathematical term for the significant figures that a number has. You can just think of this as the bits that actually represent the values in the number instead of where the decimal goes or whether the number is positive or negative.
dherman on GitHub has a cool explorer for how the bits are used.
It’s ok if you don’t totally understand how each of these bits are used. What is important to understand is that if we want precise integers in JavaScript we don’t have all 64 bits available. And even if we did, as is the case with many other programming languages, 264 is still only 9,223,372,036,854,775,808. So how do we go about representing integers bigger than that? To answer that question, let’s look at an approach to adding integers that might look familiar.
The Decimal System
If I think back to learning about simple addition and subtraction of numbers in elementary school, I remember my teachers talking about the different columns of a number that represent the different orders for magnitude. For example, with the number 123, 3 is in the “one’s column”, 2 (or twenty) is in the “ten’s column”, and 1 (or 100) is in the “hundreds column”.
Another way of thinking about this is that each column in a decimal number is the number multiplied by a power of ten. So for 123, we have:
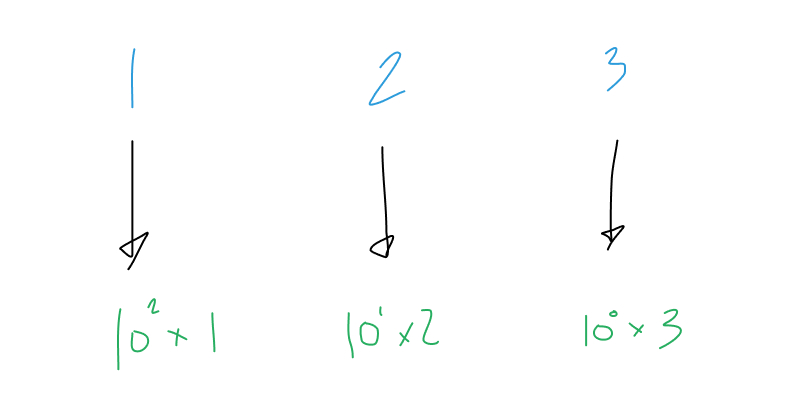
Recall that any number to the 0th power is
1so 100 is just1.
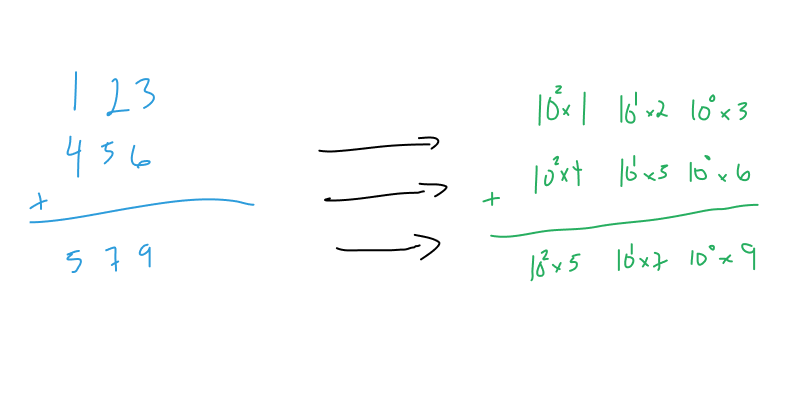
When we add numbers with multiple columns, we match up the columns with their corresponding orders of magnitude.
I will not be apologizing for my handwriting at this time, but thank you for thinking about it.
Carrying Digits
What happened when adding two numbers in a single column whose sum was 10 or more? A 1 had to be carried from the previous column to the column an order of magnitude higher.
This process of carrying and representing numbers as a composition of orders of magnitude is exactly what we need to understand how we can act on large numbers in JavaScript.
Using Orders of Magnitude to Represent Large Integers
While JavaScript might not have native support (yet!) for integers that are larger than the largest precise integer (253), we can use another data structure to precisely represent integers: arrays! Specifically, we can use each element in the array as the digit of the number at a given power of ten.
Implementing a Small Constructor for Handling Big Numbers
To make things easier on the math, let’s make it so that the numbers in our array are in reverse order so that each index corresponds to the power of ten the digit represents. So to represent 123, we would use the array [3,2,1] so that the column that represents 100 is at index 0 (3), the column that represents 101 is at index 1 (2), and the column that represents 102 is at index 2 (1).
Let’s encapsulate this idea into a JavaScript constructor function, which has one property for now, an integer represented by an array with each element representing a digit and its corresponding power of 10.
function BigInt(intArray) {
this.value = intArray;
}
// Create sample number
var int = new BigInt([3,2,1]); // Represents 123
Let’s also add a way of displaying this number in a more readable form by creating a method that prints a string that is the integer in its entirety (and has the digits ordered intuitively):
function BigInt(intArray) {
this.value = intArray;
this.toString = function convertArrayToString() {
var numString = '';
for (var i = this.value.length - 1; i >= 0; i--) {
numString += this.value[i];
}
return numString;
};
return this;
}
// Create sample number
var int = new BigInt([3,2,1]);
var intStr = int.toString(); // => returns '123'
See the Pen BigInt Demo 1 by Joe Lipper (@joelip) on CodePen.
The largest integer we can represent in JavaScript precisely is 9007199254740992. With any number higher than this, we get behavior that we don’t want. For example, adding one to this number still yields 9007199254740992. Test it out below:
See the Pen Misbehaving large numbers by Joe Lipper (@joelip) on CodePen.
Before we extend our BigInt class to handle addition so we can do precise calculations on numbers bigger than 9007199254740992, let’s make it easier to pass in integers by allowing our constructor to also accept a string of the number and assigning it to the proper properties. This will save us from having to write out longer arrays as numbers get bigger:
function BigInt(value) {
this.value = parseValue(value);
this.toString = function convertArrayToString() {
var numString = '';
for (var i = this.value.length - 1; i >= 0; i--) {
numString += this.value[i];
}
return numString;
};
function parseValue(value) {
if (Array.isArray(value)) return value;
if (typeof value === 'string') {
var result = [];
intString.split('').forEach(function(digit) {
result.unshift(parseInt(digit, 10)); // make sure we add values in reverse order
});
return result;
}
throw new Error('Value must be an array or a string.');
}
return this;
}
The general algorithm for addition that we’ll use is essentially following how we did addition using the tens columns earlier: for each digit in each integer, add all digits with a corresponding order of magnitude. Since we need to reach all digits in our numbers, we can use a loop to go through them.
function BigInt(value) {
//...
this.add = function(addend) {
var a = this.value;
var b = parseValue(addend); // need to make sure our input is an array also
for (var i = 0; i < b.length; i++) {
var currentSum = a[i] + b[i];
a[i] = currentSum;
}
this.value = a;
return this;
};
//...
}
var int = new BigInt('1234');
int.add('20006')
int.toString();
We’re heading in the right direction, but there cases where this approach falls apart:
- What happens when
ahas a greater length thanb? What about vice-versa? - When we have two numbers at an index that add up to 10 or more, we need to carry the 1 into the next column. How can we accommodate that?
- What happens when a carry goes into a column that is greater than the length of either array (as was the case in our our diagram above)?
Note: another flaw in our
addmethod is that it can’t handle negative numbers. Since adding a positive number to a negative number is equivalent to subtraction, I’m going to forego discussing it in this post. I may expand this post later to handle more operations or break it up into multiple posts that deal with each arithmetic operation. If you want to see how someone else implemented it, I recommend looking through BigInteger.js’s implementation.
Handling Numbers of Different Lengths
One way we could handle numbers of different lengths is by figuring out which one is longer (has more columns) and adding the shorter one to each digit until we run out of digits to add. At that point we can just retain the values of whatever the longer number has in its columns where there is no corresponding value.
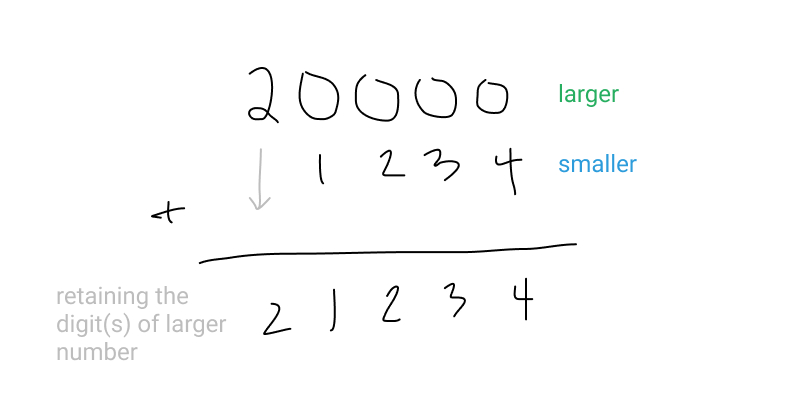
Here’s how we could translate this to code:
function BigInt(value) {
//...
this.add = function(addend) {
var a = this.value;
var b = parseValue(addend); // need to make our input is an array also
var largerArray = a.length >= b.length ? a : b;
var smallerArray = largerArray === a ? b : a; // See #1 below
for (var i = 0; i < largerArray.length; i++) {
if (typeof smallerArray[i] !== 'undefined') largerArray[i] += smallerArray[i];
// See #2 below
}
this.value = largerArray;
return this;
};
//...
}
var int = new BigInt('1234');
int.add('20000');
int.toString();
This works! A couple of notes about this approach:
- At
#1during the assignment ofsmallerArray, we’re not comparing the size of the arrays because what we really need is the other array that isn’tlargerArray. This makes sure we’re always adding two different arrays, even when they’re of equal length. - At
#2, we’re only computing the sum of the two corresponding elements in the array, if there is a column for it in the smaller array. Otherwise, we’re not updating the element’s value.
When we run this with a number that carries a digit:
var int = new BigInt('1234');
int.add('20006');
int.toString();
We get a result we don’t want with the ten sitting in the ones column. Let’s fix that.
Handling Carried Digits
We’ll approach carrying by checking to see if the sum of the elements is greater than our base (which is 10, or the threshold at which we need to carry a 1), and if it is, we’ll:
- increment the number at the next order of magnitude (i.e. the number at the next index)
- subtract our base (
10) from the current spot so that whatever is in the one’s column is leftover
function BigInt(value) {
var BASE = 10;
//...
this.add = function(addend) {
var a = this.value;
var b = parseValue(addend);
var largerArray = a.length >= b.length ? a : b;
var smallerArray = largerArray === a ? b : a;
for (var i = 0; i < largerArray.length; i++) {
if (typeof smallerArray[i] !== 'undefined') largerArray[i] += smallerArray[i];
if (largerArray[i] >= BASE) {
largerArray[i + 1] += 1; // carry one into next column
largerArray[i] -= BASE; // leave only the one's column for the carried value
}
}
this.value = largerArray;
return this;
};
//...
}
var int = new BigInt('1234');
int.add('20006');
int.toString();
We’re almost at a working solution, but we still need to figure out what to do if we get a carried 1 into a column that is longer than either number. If we don’t account for adding an element to the array representing our integer in this case, then we’ll end up with NaN as the first “digit” of our number:
var int = new BigInt('91234');
log(int);
log(int.add('21806').toString()); // "NaN13040"
We can handle this by either incrementing the element in the position of the carry column, or assigning it with 1, like this:
function BigInt(value) {
var BASE = 10;
//...
this.add = function(addend) {
var a = this.value;
var b = parseValue(addend);
var largerArray = a.length >= b.length ? a : b;
var smallerArray = largerArray === a ? b : a;
for (var i = 0; i < largerArray.length; i++) {
if (typeof smallerArray[i] !== 'undefined') largerArray[i] += smallerArray[i];
if (largerArray[i] >= BASE) {
largerArray[i + 1] = ++largerArray[i + 1] || 1; // carry one into next column,
// OR assign a one to our new column
largerArray[i] -= BASE; // leave only the one's column for the carried value
}
}
this.value = largerArray;
return this;
};
//...
}
With this approach, we can try adding one to the largest JavaScript integer and see what we get with our solution:
See the Pen BigInt Demo with Add by Joe Lipper (@joelip) on CodePen.
Closing Notes
The idea of using an element’s index in an array to represent orders of magnitude is something that is useful for implementing subtraction and multiplication as well. If you’re looking to expand upon the learnings in this post, I recommend starting there! Division can get considerably hairier, though, so keep that in mind if you’re looking to write a fully functional library.
Luckily, the tediousness of dealing with big integers in this post will be alleviated with the release of the BigInt support in future versions of V8. Performing arithmetic operations with arbitrarily-sized ints will be as easy as adding an n to the end of any integer:
1234567890123456789n * 123n;
// → 151851850485185185047n ✅
From the post announcing BigInt support.
If you’re looking to learn more about how you can use BigInts in V8 (and Chrome), I highly recommend reading the high-level release post (linked multiple times in this post) and also their more technical post on the V8 blog.
The source code for this post can be found on my GitHub. I’m also looking for a job right now, so if you’re hiring people who like to write and think about software in this way, I’d love to hear from you.
Some other resources that were helpful/interesting in my research for this post:
- This post on Large Integer Arithmetic
- This research paper on efficient algorithms for cryptography
- Mozilla’s progression of adding support for BigInts
- The TC39 proposal of
BigInt - This Medium post on JavaScript’s
Numbertype - Section 3.5 of Computer Organization and Design which is great primer on how all this stuff works on a hardware level
- All hand drawings were done with the pencil tool in Figma.